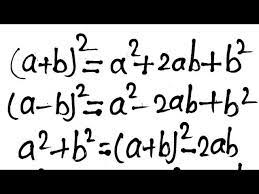If you’ve ever come across the formula (a^2 + b^2) in your math class, you might wonder what it actually means and why it’s important. Let’s break down this expression in simple terms and see where it shows up in real-life situations.
What Is the (a^2 + b^2) Formula? A Simple Explanation
What Does (a^2 + b^2) Mean?
The expression (a^2 + b^2) is made up of two parts:
- (a^2): This means “a squared,” or (a) multiplied by itself. For example, if (a = 3), then (a^2 = 3 \times 3 = 9).
- (b^2): This means “b squared,” or (b) multiplied by itself. If (b = 4), then (b^2 = 4 \times 4 = 16).
So, (a^2 + b^2) is just the sum of these two squared numbers. There isn’t a trick to simplifying it further without more context—it’s simply adding the square of (a) to the square of (b).
Where Do We Use (a^2 + b^2)?
You might be surprised to learn how often this expression pops up in everyday math, science, and engineering. Here are some common situations where you’ll see (a^2 + b^2):
- Geometry: The formula is at the heart of the Pythagorean theorem. This theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides:
[
a^2 + b^2 = c^2
]
This is used to find the length of any side of a right triangle if you know the lengths of the other two sides. - Distance Between Points: In coordinate geometry, you can use (a^2 + b^2) to calculate the distance between two points on a grid. The distance formula, which is derived from the Pythagorean theorem, is:
[
\text{Distance} = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}
]
Here, (a^2 + b^2) is used to find the straight-line distance between two points. - Physics and Engineering: In physics, you might use this formula to calculate the magnitude of a vector or the total energy in a system. For example, when calculating the kinetic energy of two moving objects, you might use their speeds in this squared form.
Related Formulas Involving (a^2 + b^2)
While (a^2 + b^2) is a straightforward expression, it connects to other useful formulas:
- Square of a Sum:
[
(a + b)^2 = a^2 + 2ab + b^2
]
This tells us how to expand the square of the sum of two numbers. - Square of a Difference:
[
(a – b)^2 = a^2 – 2ab + b^2
]
This shows how to expand the square of the difference between two numbers.
Real-Life Example: Calculating Distance
Imagine you want to find the shortest distance between two locations on a map. Let’s say one location is at (3, 4) and the other is at (6, 8). To calculate the straight-line distance between these two points, you can use the distance formula:
[ \text{Distance} = \sqrt{(6 – 3)^2 + (8 – 4)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 ]
This formula tells us that the distance between the two points is 5 units.
Q. What is a2- b2 formula?
The formula of the Subtraction of squares or a²- b² formula is (a²- b²) =(a+b)(a-b)
Q. How should the a2 + b2 Formula be used?
To determine whether two terms have the power of 2 or not, first look at the pattern of terms provided in the question.
If it is in the form a2 + b2, then use the sum of squares formula a2 + b2 = (a + b)2 -2ab, substituting the values of a and b.
Q. Where does the a2 b2 formula come from?
a2 + b2 is the sum of the squares of a and b.
Using the algebraic identity (a+b)² = a²+ b² + 2ab, we could derive the formula of a2 + b2.
a2 + b2 = (a + b)² -2ab is the result of substituting 2ab from both sides.
Conclusion
The (a^2 + b^2) formula might seem simple, but it’s incredibly versatile and shows up in many areas of math and science. Whether you’re calculating distances, working with geometric shapes, or solving physics problems, understanding how to use this expression is a valuable skill.
So, next time you see (a^2 + b^2), you’ll know exactly what it means and how you can use it to solve real-world problems!